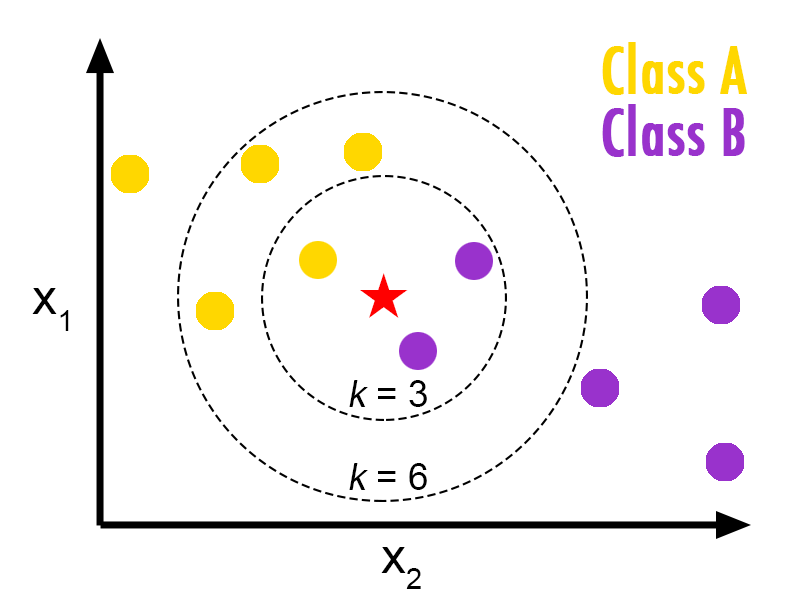
In this Lab you will load a customer dataset, fit the data, and use K-Nearest Neighbors to predict a data point. But what is K-Nearest Neighbors?
K-Nearest Neighbors is an algorithm for supervised learning. Where the data is 'trained' with data points corresponding to their classification. Once a point is to be predicted, it takes into account the 'K' nearest points to it to determine it's classification.
In this case, we have data points of Class A and B. We want to predict what the star (test data point) is. If we consider a k value of 3 (3 nearest data points) we will obtain a prediction of Class B. Yet if we consider a k value of 6, we will obtain a prediction of Class A.
In this sense, it is important to consider the value of k. But hopefully from this diagram, you should get a sense of what the K-Nearest Neighbors algorithm is. It considers the 'K' Nearest Neighbors (points) when it predicts the classification of the test point.
How does K-Mean algorithm works?
K-Means algorithm is used for identifying clusters in a given dataset. For this learning sake, let’s assume that we have 2 independent variables (plotted on X & Y). Each point of the dependent variable is plotted on graph.
Step 1 :- Decide on number of cluster you want. For this e.g, let’s take K = 2
Step 2 :- Based on the chosen cluster, identify the points as center points. In this case, identify any 2 points on the graph and mark them as center points (C1, C2).
Step 3 :- Now, for each data point, classify them into 1st or 2nd cluster based on the closest point. For e.g, a point of (2,5) may be closest to center C1 than to center C2. In this case, point (2,5) will be marked into a cluster which has a center point as C1.
Step 4 :- After classifying all data points into C1 or C2, now you will have few points which are close to C1 and rest are close to C2. Based on these points, calculate new center point for data points which were in C1 group. So, C1 will move to a new point. The same will happen to C2.
Step 5 :- Repeat Step 3, Step 4 until a point is reached where C1 & C2 don’t move any further!
Thants K-Means for you!
Lets load required libraries
import itertools
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import NullFormatter
import pandas as pd
import numpy as np
import matplotlib.ticker as ticker
from sklearn import preprocessing
%matplotlib inline
About the dataset
Imagine a telecommunications provider has segmented its customer base by service usage patterns, categorizing the customers into four groups. If demographic data can be used to predict group membership, the company can customize offers for individual prospective customers. It is a classification problem. That is, given the dataset, with predefined labels, we need to build a model to be used to predict class of a new or unknown case.
The example focuses on using demographic data, such as region, age, and marital, to predict usage patterns.
The target field, called custcat, has four possible values that correspond to the four customer groups, as follows: 1- Basic Service 2- E-Service 3- Plus Service 4- Total Service
Our objective is to build a classifier, to predict the class of unknown cases. We will use a specific type of classification called K nearest neighbour.
Lets download the dataset. To download the data, we will use !wget to download it from IBM Object Storage.
!wget -O teleCust1000t.csv https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/ML0101ENv3/labs/teleCust1000t.csv
Did you know? When it comes to Machine Learning, you will likely be working with large datasets. As a business, where can you host your data? IBM is offering a unique opportunity for businesses, with 10 Tb of IBM Cloud Object Storage: Sign up now for free
df = pd.read_csv('teleCust1000t.csv')
df.head()
Data Visualization and Analysis
df['custcat'].value_counts() #cuscat is out dependent variable here
You can easily explore your data using visualization techniques:
df.hist('income', bins=10, color = 'orange', range = (0,1250))
Lets define feature sets, X:
df.columns
To use scikit-learn library, we have to convert the Pandas data frame to a Numpy array:
X = df[['region', 'tenure','age', 'marital', 'address', 'income', 'ed', 'employ','retire', 'gender', 'reside']] .values #.astype(float)
X[0:5]
What are our labels?
y = df['custcat'].values
y[0:5]
Data Standardization give data zero mean and unit variance, it is good practice, especially for algorithms such as KNN which is based on distance of cases:
from sklearn.preprocessing import StandardScaler
X = StandardScaler().fit_transform(X.astype(float))
X[0:5]
Train Test Split
Out of Sample Accuracy is the percentage of correct predictions that the model makes on data that that the model has NOT been trained on. Doing a train and test on the same dataset will most likely have low out-of-sample accuracy, due to the likelihood of being over-fit.
It is important that our models have a high, out-of-sample accuracy, because the purpose of any model, of course, is to make correct predictions on unknown data. So how can we improve out-of-sample accuracy? One way is to use an evaluation approach called Train/Test Split. Train/Test Split involves splitting the dataset into training and testing sets respectively, which are mutually exclusive. After which, you train with the training set and test with the testing set.
This will provide a more accurate evaluation on out-of-sample accuracy because the testing dataset is not part of the dataset that have been used to train the data. It is more realistic for real world problems.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.2, random_state=4)
print ('Train set:', X_train.shape, y_train.shape)
print ('Test set:', X_test.shape, y_test.shape)
Classification
K nearest neighbor (KNN)
Classifier implementing the k-nearest neighbors vote.
from sklearn.neighbors import KNeighborsClassifier
neigh = KNeighborsClassifier(n_neighbors = 38).fit(X_train, y_train)
neigh
yhat = neigh.predict(X_test)
yhat[0:5] #this will print the classes of out end dependent variable
from sklearn.metrics import accuracy_score , confusion_matrix, classification_report
#print('Train set Accuracy:' , accuracy_score(y_train , neigh.predict(X_train)))
print('::::Test set sccuracy:::::' , accuracy_score(y_test, yhat))
print(':::::Confusion Matrix:::::','\n',confusion_matrix(y_test, yhat))
print(':::::Classification Report:::::','\n', classification_report(y_test, yhat))
Evaluating Results
- As we can see our accuracy report is very bad having only 0.32% accuracy
- In the classification report the precision is only 0.37 and recall is 0.45 which are below average
- We can get better results when we have the right value of k which is a hyperparameter here
- Please follow the code in next section to find the best k
What about other K?
K in KNN, is the number of nearest neighbors to examine. It is supposed to be specified by the User. So, how can we choose right value for K? The general solution is to reserve a part of your data for testing the accuracy of the model. Then chose k =1, use the training part for modeling, and calculate the accuracy of prediction using all samples in your test set. Repeat this process, increasing the k, and see which k is the best for your model.
We can calculate the accuracy of KNN for different Ks.
*Note - I also used elbow method here, It worked fine for me in finding the best case.* </>
Ks=50
mean_acc=np.zeros((Ks-1))
std_acc=np.zeros((Ks-1))
ConfustionMx=[];
for n in range(1,Ks):
#Train Model and Predict
kNN_model = KNeighborsClassifier(n_neighbors=n).fit(X_train,y_train)
yhat = kNN_model.predict(X_test)
mean_acc[n-1]=np.mean(yhat==y_test);
# np.mean(y_test==y_pred) first checks if all the values in y_test is equal to corresponding values
# in y_pred which either results in 0 or 1. And then takes the mean of it (which is still 0 or 1).
std_acc[n-1]=np.std(yhat==y_test)/np.sqrt(yhat.shape[0])
plt.plot(range(1,Ks),mean_acc,'g')
plt.fill_between(range(1,Ks),mean_acc - 1 * std_acc,mean_acc + 1 * std_acc, alpha=0.10)
plt.legend(('Accuracy ', '+/- 3xstd'))
plt.ylabel('Accuracy ')
plt.xlabel('Number of Nabors (K)')
plt.tight_layout()
plt.show()
print( "The best accuracy was with", mean_acc.max(), "with k=", mean_acc.argmax()+1)